We consider here the approach formalism as it was given in [4] in its applications to the CERES Silicon Drift detector (SiDD). As it was shown
in [5] the bell-shape form of the signal with reasonable
assumption can be treated as a two-dimensional Gaussian with the maximum
amplitude A.
The digitized signal can be considered as two-dimensional histogram
![]() formed by extracting cluster of adjacent cells with
amplitudes exceeding a given threshold. However due to the factorial
view of 2D Gaussian we can reduce this 2D problem to several
one-dimensional ones
formed by extracting cluster of adjacent cells with
amplitudes exceeding a given threshold. However due to the factorial
view of 2D Gaussian we can reduce this 2D problem to several
one-dimensional ones ![]() , which we
suppose having the unit bin size,
i.e.
, which we
suppose having the unit bin size,
i.e. ![]() .
.
In order to estimate the center and the amplitude of a signal we have to fit
this histogram with the function ![]() ,
where D is supposed to be known. The iterative solution of the corresponding
least square functional
,
where D is supposed to be known. The iterative solution of the corresponding
least square functional
![]() is elaborated in [4] on the basis of approximating
is elaborated in [4] on the basis of approximating
![]() by an elliptic paraboloid. As initial values
by an elliptic paraboloid. As initial values ![]() of unknown
parameters for this procedure in a single signal case we use
maximum amplitude of input data and its position or the histogram center of
gravity. Further we refer to this method as to Paraboloidal
Approximation Method (PAM).
of unknown
parameters for this procedure in a single signal case we use
maximum amplitude of input data and its position or the histogram center of
gravity. Further we refer to this method as to Paraboloidal
Approximation Method (PAM).
Analysing the PAM accuracy we use the standard maximum likelihood method (MLM)
for estimating the signal amplitude A and location parameter ![]() and
apply the famous Cramer-Rao inequality [6]
for low limit of these parameters estimation accuracy.
Under conditions of the negligible correlation between
and
apply the famous Cramer-Rao inequality [6]
for low limit of these parameters estimation accuracy.
Under conditions of the negligible correlation between ![]() and A and for
and A and for
![]() and the gaussian shape of signals
and the gaussian shape of signals
![]() we obtain
we obtain
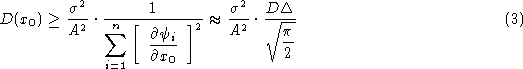
and its approximate estimation
![]()
If ![]() , D=4,
, D=4, ![]() , one has
, one has ![]()
The shape of a signal produced by two superimposing peaks can be described like
The minimized functional depends now on four parameters. Its minimization was done in [4] by direct generalization of the PAM procedure. The important innovation of the given paper is the idea to use, as initial values of parameters, results obtained by the non-parametric algorithm. Such combined NP-PAM method improves considerably the accuracy and reliability of the whole procedure.

Fig.1 The numerical test of two peaks reconstruction from the 16 bins histogram, size of 1 bin equal 32; a) input data: histogram - 1, instrumental function - 2, SNR=60 dB; b) output data: solid line 1 is presented the original peaks, black squares 2 are presented the reconstructed peaks by DCONV program [3]. The insert shows distribution of deviations between simulated and estimated peak positions obtained by the parametric PAM algorithm with starting values provided by non-parametric algorithm.